REWARD SHAPING

RESL previously explored using OpenAI’s implementations of various algorithms but had the most success with Proximal Policy Optimization (PPO). Thus, as we began development, we chose to further explore PPO. To begin leading the quadrotor to effectively perform path following, we first focused on directly extending RESL’s PPO work by evaluating different reward functions.


Original Reward Function:

Originally, the reward function penalized the quadrotor based on a number of different factors, including

Distance between quadrotor’s position and goal position

The amount of control effort exerted by the quadrotor

Whether the quadrotor crashed or not

Orientation along the Z axis

Yaw

Uncontrolled rotation about the Z axis

How drastically the rotor thrusts in the current action differed from those of the previous action

Velocity

Attitude

Restructuring Goal Representation

RESL previously trained the quadrotor to hover at a specific point with its z orientation perpendicular to the xy-plane. To do so, they provided one goal point to the environment. In order to adapt the environment to represent a goal trajectory, we added support for multiple goals. Additionally, we updated the visualization tool to show multiple goals and change the color of each goal reached by the quadrotor. Figure 3 shows two goals in the visualization tool.

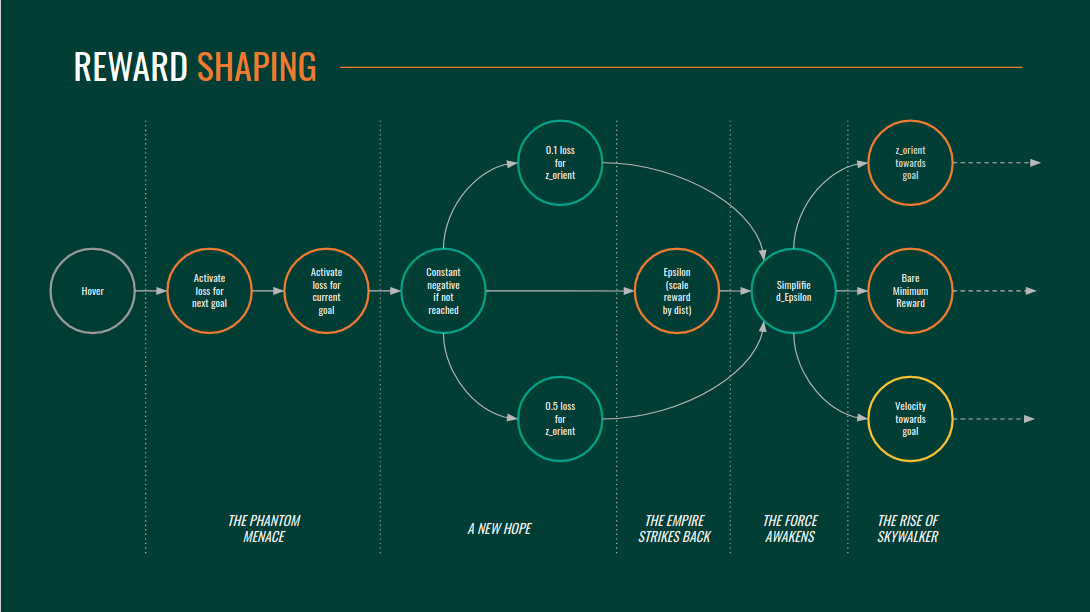
Different Reward Shaping Strategies:

• Activate loss to next goal when the previous is reached.

  • Description:

    In this approach, we disregarded the error in position between the quadrotor and goals farther along in the given trajectory until the quadrotor came within a certain radius of the preceding goals. This is the most straightforward reward which we could use for multiple goals. Since the loss to each subsequent goal is scaled by 2, the quad should care more about getting to this next goal then staying at the last one.
  
  

  • Result:

    The controller doesn’t perform well. As soon as the quad reaches the first goal, we start adding the loss to the second goal. This means that it gets a sudden negative reward if it reaches, so the controller just learns to stop right outside the tolerance where it reaches the goal.



• Only current goal is active.

  • Description:

    Since the quadrotor does not need to return to previously reached goals, the reward function only factors in loss for the subsequent goal.
  
  

  • Result:

    As the quadrotor reaches a goal point, it again gets a negative reward since the loss to the subsequent goal gets factored into the reward function, so it again learns to hover outside of the radius of tolerance and does not learn to navigate through the given goal points.



• Add a constant negative reward for each goal which is not yet reached.

  • Description:

    In the earlier reward functions the quadrotor received a negative reward for the following goal when it reaches the current one. To address this issue, we add a constant negative reward for each goal which is not yet reached. When the quadrotor reaches a goal, the constant negative reward is removed and replaced with the loss to the next goal.
  
  

  • Result:

    This reward function worked well and the quadrotor was finally able to reach the second goal as it was not penalized for reaching each of the target goal points like before by simply the addition of loss to the next goal point. The addition of a constant negative reward for each goal not reached and the removal of this loss when it reached the point rewarded the quad well and helped it learn to follow the given path.



• Epsilon.

  • Description:

    Our vanilla reward function (described above) simply activated losses for the next goal once a goal has been reached. We came up with an alternative approach where instead of losses being turned on/off using flags, the weight of the loss decreased the closer the quadrotor to that goal. In other words, the error (loss) in position for the current goal would be defined by:
    loss_position = epsilon_min * E_dist
    epsilon_min = min(epsilon_min, E_dist)
    Where E_dist is simply the norm of the difference between the position of the goal and the position of the quad. Having the reward scale in this fashion effectively allowed the reward function to “remember” how close the quad got to the goal and assign a reward based on that value.
  
  

  • Result:

    Although this reward type seemed promising, the plots average reward and average discounted reward was extremely noisy and failed to converge even after prolonged training. We think the nonlinearity that was introduced by epsilon_min is the primary cause of this.



• Simplified Epsilon.

  • Description:

    The motivation for the previous reward function was to scale the loss for the first goal proportional how close you got to that goal. This also changed how sensitive the reward is to the change in position since the position loss now depends on both the distance to the goal, and the scaling factor (which again is a function of the distance to the goal). For this reward, the intuition was to remove this effect while still being able to incorporate the minimum distance to goal. For this, instead of multiplying the min distance to the current distance to goal, we just used the min distance itself to calculate the position loss.
  
  

  • Result:

    The quadrotor reaches both goals but in a suboptimal manner.



• Velocity in direction of the goal.

  • Description:

    The intuition for this reward type stems from the notion that an optimal trajectory would be one that gets to both goals the fastest. In order to reward this behavior, we added a velocity component to the loss. Specifically, we assigned a continuous loss of lossvelocity = Vproj , where denotes the weight of the losses relative to the other losses (set to 1 in this case), and V_proj is the velocity of the quadrotor in the direction of the next goal.
  
  

  • Result:

    This reward function ultimately proved to be unsuccessful.



• Z-Axis Orientation Loss.

  • Description:

    We found that the quadrotor continually attempted to remain vertically upright, keeping its z-axis orientation perpendicular to the floor, which prevented it from reaching the goal states in an optimal manner. We first attempted to reduce the degree to which the z-axis orientation loss factored into the reward function. This didn’t have a substantial effect on the quadrotor’s behavior. Additionally, we trained the quadrotor to align its z-axis orientation in the direction of the next goal position. The Z angle to goal is defined by the following equation:
    Z_{angle to goal} = arccos(dot(goal - pos_curr, pos_curr)) / (norm(goal - pos_curr) * norm(pos_curr))
  
  

  • Result:

    This did well until the quad reached the first goal although the training took time. After reaching the first goal, the quad found it hard to align itself to the second goal. We initially thought this was because it received a huge loss on reaching the first goal since the error of the orientation wrt the second goal was added. So a value of pi was added and then disabled after reaching the first goal when the error to the second goal was added. But the quad still found it hard to align itself to the second goal even in this situation. The training was done on 3000 iterations. Increasing this number could lead to a better learning which will be tried out in the future.
    We also attempted to remove the z-axis loss from the reward function after a certain number of training iterations, but this also had little to no effect on the quadrotor’s behavior.